À boire et à manger : Poêle à (la) convection
écrit le: 26 mars 2014 par admin
À boire et à manger : Poêle à (la) convection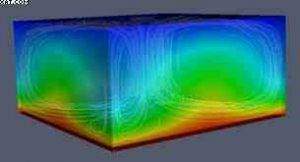
Quand on met de l’huile dans une poêle, sa surface s orne de petites cellules en nid-d’abeilles dont la taille semble dépendre de l’épaisseur de l’huile. Pourquoi ?
Les cellules que vous observez sont des cellules de convection dites de Rayleigh-Bénard. Si la différence de température entre le fond de l’huile et la surface est faible, la chaleur est dissipée par transfert thermique (collision des molécules), ce qui n’engendre aucun mouvement de l’huile. Si la différence de température augmente, la convection, un mouvement d’ensemble des molécules, devient la façon la plus efficace de transférer la chaleur. L’huile chauffée étant moins dense, elle tend à s’élever vers la surface. Là, elle se refroidit au contact de l’air, et tend à couler à nouveau. Ce mouvement circulaire crée tics petites cellules contiguës qui s’arrangent spontanément en nid-d’abeilles.
Ce phénomène – facilement observable à la cuisine – a généré beaucoup de recherches, et l’on sait aujourd’hui pourquoi la structure en nid-d’abeilles est favorisée. La forme des cellules de convection dépend de la géométrie du récipient utilisé. Des motifs hexagonaux semblent se développer de préférence dans des récipients circulaires, les autres engendrant plutôt des cellules rectangulaires de section carrée. Le mouvement cyclique du liquide (vers le haut, de côté, vers le bas, et à nouveau de côté) fait que la taille de la cellule dépend crucialement de l’épaisseur du liquide.
C’est environ 20 secondes après le début du chauffage que démarre, brutalement, la convection. Dès que le gradient de température au sein du liquide atteint un seuil critique, les divers mouvements de convection, jusque-là isolés, trouvent plus efficace du point de vue énergétique de se rassembler. En partageant par exemple avec le mouvement voisin la phase de descente, on évite à coup sûr que deux courants opposés se rencontrent. Cette auto-organisation des cellules de convection donne une structure régulière optimale. Le nid-d’abeilles, par exemple, optimise la surface de chaque cellule.
Sous l’effet de cette coopération, la convection se fait plus vigoureuse, et l’on peut voir une petite fontaine s’élever au centre de chaque cellule. La force qui assure la pérennité de cette structure, malgré les perturbations mécaniques et thermiques, est le transfert de chaleur à travers la couche d’huile. De la même façon, un système biologique ne maintient son intégrité que parce qu’il assure un transfert d’énergie – sous forme de nourriture en l’occurrence.
Une augmentation brutale de la température mène à la destruction des cellules de convection, qui passent par plusieurs phases avant de disparaître dans un chaos complet.
On peut montrer que la cellule de convection idéale pour transférer de la chaleur du fond d’une poêle vers la surface est hexagonale, chaque cellule ayant un diamètre égal à la profondeur de l’huile. Le fluide chaud s’élève au centre de la cellule, refroidit en surface, puis redescend le long des parois de l’hexagone. Des motifs semblables à ceux d’une poêle à frire sont observés à la surface du Soleil.
Le comportement de l’huile dans une poêle à frire est l’exemple classique de la convection de Rayleigh-Bénard, qui produit des cellules hexagonales entre deux plans portés à des températures différentes. On sait que lord Rayleigh, physicien britannique (1842-1919), a donné une théorie du phénomène, mais on sait moins que cette théorie était fausse.
Rayleigh considérait une couche horizontale de liquide chauffée par en dessous. Il montra que la convection prenait la forme de cellules tournant en sens opposés sous l’effet des mouvements de fluides de densités différentes. Avec des arguments purement heuristiques, il estima la taille d’une cellule et tomba par hasard sur une valeur voisine de celle trouvée r u le physicien français Henri Bénard ( 1874-1939). Il calcula aussi plus petite différence de température susceptible de provoquer la convection, mais trouva une valeur cent fois supérieur me a celle que Bénard avait déterminée expérimentalement.
D’autres expériences étendirent les analyses de Rayleigh. On comprit que la surface du fluide n’était pas plane, mais soulevée à l’aplomb des remontées de fluide, et abaissée aux endroits où il plonge vers le fond. Or, Bénard observa exactement le contraire ! Il montra en outre que les cellules se lui niaient aussi quand on diminuait la température du fond, .ilois que Rayleigh prévoyait un arrêt du mouvement. L’instabilité a été observée en plaçant le liquide en dessous d’une plaque chauffante, et même dans l’espace, en gravité zéro !
A la fin des années 1950, un nouveau modèle pour la convection de Bénard expliqua que les mouvements de convection fiaient en fait dus aux variations de la tension superficielle engendrée par les différences de température. Ce modèle prévoyait aussi un affaissement des centres des cellules de convection. En réalité, Rayleigh et Bénard avaient tous deux raison, l’effet de l’un ou de l’autre dominant selon les circonstances extérieures. Les forces de densité prédominent quand il n’y a pas de surface libre, ou quand l’épaisseur du fluide dépasse 10 millimètres; dans les autres cas, c’est la tension superficielle qui l’emporte.
Quelles que soient les conditions de l’expérience, la force responsable de la convection doit surmonter le frottement visqueux avant de provoquer le mouvement du fluide. Pour les mouvements de densité, c’est le «nombre de Rayleigh» (rapport des forces de densité aux frottements) qui détermine le début de l’instabilité, alors que pour les mouvements dus à la tension superficielle, c’est le «nombre de Marangoni» (rapport des forces de tension aux frottements).
Pour les couches fines de fluides, l’instabilité de Rayleigh Bénard donne des cellules hexagonales quelle que soit la forme du récipient. Pour des épaisseurs plus grandes, on observe une série de rouleaux d’axes parallèles aux parois. Quand la température augmente, ils prennent des formes polygonales, mais pas nécessairement hexagonales.
Vidéo: À boire et à manger : Poêle à (la) convection
Vidéo démonstrative pour tout savoir sur: À boire et à manger : Poêle à (la) convection

